Question

A curve in a road forms part of a horizontal circle. As a car goes around it at constant speed 14.0 m/s, the total horizontal force on the driver has magnitude 130 N. What is the total horizontal force on the driver if the speed on the same curve is 18.0 m/s instead?

Answer 1

Step-by-step explanation:

It is given that,

Initial speed, v₁ = 14 m/s

Initial force, F₁ = 130 N

We need to find the total horizontal force (F₂) on the driver if the speed on the same curve is 18.0 m/s instead, v₂ = 18 m/s

The centripetal force is given by :

`F=(mv^2)/(r)`

`(F_1)/(F_2)=(mv_1^2/r)/(mv_2^2/r)`

`(F_1)/(F_2)=(v_1^2)/(v_2^2)`

`F_2=(v_2^2* F_1)/(v_1^2)`

`F_2=((18\ m/s)^2* 130\ N)/((14\ m/s)^2)`

`F_2=214.8\ N`

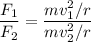
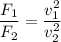
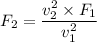
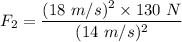
So, if the speed is 18 m/s, then the horizontal force acting on the car is 214.8 N. Hence, this is the required solution.