Question

Part A: A charge +Q is located at the origin and a second charge, +9Q, is located at x= 15.8 cm . Where should a third charge q be placed so that the net force on q is zero? Find q 's position on x -axis.

Part B: A charge +Q is located at the origin and a negative charge, -7Q, is located at a distance x= 19.6 cm . Where should a third charge q be placed so that the net force on q is zero? Find q 's position on x-axis.

Answer 1

Part a)

x = 3.95 cm

Part b)

x = - 11.9 cm

Step-by-step explanation:

Part a)

Since both charges are of same sign

so the position at which net force is zero between two charges is given as

`(kq_1)/(r_1^2) = (kq_2)/((15.8 - r)^2)`

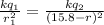
here we know that

`q_1 = Q`

`q_2 = 9Q`

`(Q)/(r^2) = (9Q)/((15.8 - r)^2)`

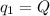
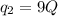
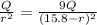
square root both sides

`(15.8 - r) = 3r`

`r = 3.95 cm`

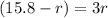
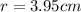
Part b)

Since both charges are of opposite sign

so the position at which net force is zero will lie on the other side of smaller charges is given as

`(kq_1)/(r_1^2) = (kq_2)/((19.6 + r)^2)`

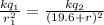
here we know that

`q_1 = Q`

`q_2 = -7Q`

`(Q)/(r^2) = (7Q)/((19.6 + r)^2)`

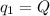
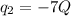
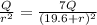
square root both sides

`(19.6 + r) = 2.64r`

`r = 11.9 cm`

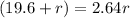
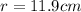
so on x axis it will be at x = - 11.9 cm