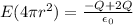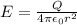Answer:
i)

ii)
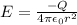
iii) E = 0
iv)
Step-by-step explanation:
1) Electric field inside uniformly charged ball
By Gauss law we will have
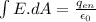
now we have
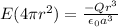

2) Electric field outside the ball and inside the shell
By Gauss law we will have
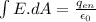
now we have

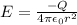
3)Electric field inside the metallic shell
E = 0
As we know that inside the conductor net electric field is always zero
4)Electric field outside the shell
By Gauss law we will have
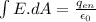
now we have