Question

Optics (Lens) Problem A lens forms an image of an object. The object is 16.0cm from the lens. The image is 12cm from the lens on the same side as the object. a. What is the focal length of the lens? Is the lens converging or diverging? b. If the object is 8.5mm tall, how tall is the image? Is it erect or inverted? c. Draw a principal ray diagram.

Answer 1

Part a)

`f = -48 cm`

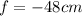
Since focal length is negative so its a diverging lens

Part b)

`h_i = 6.375 mm`

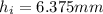
Since the magnification is position for diverging lens so it is ERECT

Step-by-step explanation:

Part a)

As we know by lens formula

`(1)/(d_i) + (1)/(d_o) = (1)/(f)`

`-(1)/(12cm) + (1)/(16) = (1)/(f)`

`f = -48 cm`

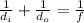
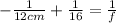
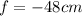
Part b)

Since focal length is negative so its a diverging lens

Part c)

As we know that

`(h_i)/(h_o) =(d_i)/(d_o)`

`(h_i)/(8.5 mm) = (12)/(16)`

`h_i = 6.375 mm`

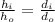
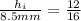
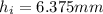
Part d)

Since the magnification is position for diverging lens so it is ERECT

Part e)