Answer:
See proof below.
Explanation:
Note:
I think you mean that f(x) = (x + 3)/2, which is
 and not what you wrote which means
and not what you wrote which means
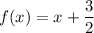
To prove that functions f(x) and g(x) are inverses of each other, you must do the composition of functions f and g, and then the composition of functions g and f. If both compositions give you the result of just x, then the functions are inverses of each other.
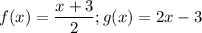
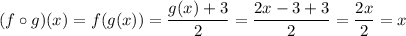
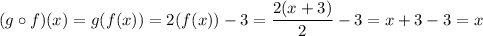
Since both compositions result in x, functions f(x) and g(x) are proved to be inverses of each other.