Proof and Explanation:
- Here, consider the product of 2 elements 'MN' as
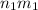 and
and
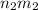 where
where
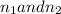 ∈ N and
∈ N and
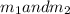 ∈ M
∈ M
The product is given as:
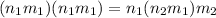
 ∈ G and
∈ G and
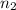 ∈ N wher N ≤ G
∈ N wher N ≤ G
and
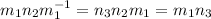
⇒
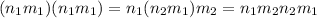
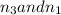 ∈ N and
∈ N and
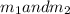 ∈ M
∈ M
The product is in NM, under multiplication NM is closed
Now, we will consider the inverse of element of an element of NM as
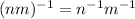
Using normality to note
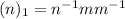 ∈ N
∈ N
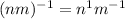
under inversion NM is closed
- Now, to show NM is normal in G, for any g ∈ G, mn ∈ MN
and also gmn
 ∈ MN
∈ MN
so, gmn
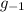 = (gm
= (gm
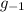 )(gn
)(gn
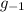 )
)
Here, first term belongs to M and the second term to N
⇒ gmn
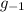 ∈ MN
∈ MN
Hence proved that MN is a normal sub group of 'G'