Question

If you invest $1000 for 20 years at an 8% nominal annual interest rate how much will you earn with monthly compounding? Daily compounding? Weekly compounding? How much difference is there between daily and weekly compounding? How much is the difference between the monthly and the daily compounding earnings?

Answer 1

a) monthly compounded value = $ 4926.80

b) weekly compounded value = $ 4946.93

c) daily compounded value = $ 4952.23

Explanation:

investment = $1000

time = 20 years

rate of interest = 8%

a) compounded monthly

`A = P * (1+i)^n`

`A = 1000 * (1+(0.08)/(12))^(20 * 12)\\A= \$ 4926.80`

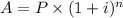
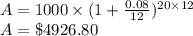
b) for weekly compounding

`A = P * (1+i)^n`

`A = 1000 * (1+(0.08)/(52))^(20 * 52)\\A= \$ 4946.93`

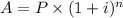
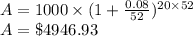
c) for daily compounding

`A = P * (1+i)^n`

`A = 1000 * (1+(0.08)/(365))^(20 * 365)\\A= \$ 4952.23`

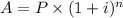
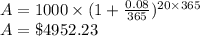
difference b/w daily and weekly compounding

= $ 4952.23- $ 4946.93 = $5.30

difference b/w monthly and daily compounding

= $ 4952.23 - $ 4926.80 = $25.43