Question

If f(x) = -1/x, then f'(x) = 1/x^2. Theorem seems to suggest that the integral from -1 to 1 of 1/x^2 dx would equal f(1) - f(-1) = -1 -1 = -2. But 1/x^2 is a positive function and so its integral over [-1,1] should be positive. What is wrong here?

Answer 1

The flaw is at x=0 where the function is not defined

Explanation:

For any function we have

`F(x)=\int f(x)dx`

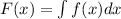
The integral can be evaluated only if the function f(x) is defined in the interval [a,b] in which this integral is evaluated

In our our case function f(x) is not defined at x=0 in the interval [-1,+1] thus this results in the flaw that we have obtained in the reasoning