If
 is a homomorphism, then we have, for every
is a homomorphism, then we have, for every
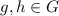
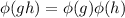
Since G is abelian, we have
 , and thus
, and thus

But we also have

which proves that G' is abelian.
In other words, for every
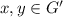 , you have
, you have
 , because there exist
, because there exist
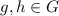 such that
such that
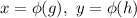 , and you can think of
, and you can think of
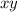 as
as
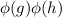 , and of
, and of
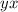 and
and
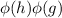
Then, you observe that
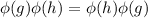 because they mean
because they mean
 , and
, and
 by hypothesis, because G is abelian.
by hypothesis, because G is abelian.