Question

I am in a mathematics for elementary school teachers classthat is online and I am not understanding any of it. Here is aproblem that I am stuck on right now. Keep in mind I must show mywork.

Consider an experiment of drawing two cards withoutreplacement from an ordinary deck of 52 playing cards.
What are the odds in favor of drawing a spade or aheart?

Answer 1

Every card has the same chance of appearing, and since there are 52 card (13 for each suit), each of them has a chance of 1/52 to appear.

At the beginning, you a 26/52 = 1/2 chance of picking a spade or a heart (there are 13 spades and 13 hearts over a total of 52 cards).

Suppose you don't pick a spade or a hear (this happens in the remaining half of the cases). There are 51 cards remaining, and all 26 spades/hearts are still in the deck. So, you have a 26/51 chance of picking a spade or a heart with the second pick.

Putting everything together, you have

`P = (1)/(2)+(1)/(2)(26)/(51)`

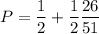
Which you should think of as "half of the times I pick a spade or a heart with the first card, the remaining half of the times I pick a spade or a heart with the second card with probability 26/51.

The expression evaluates to

`P = (1)/(2)+(1)/(2)(26)/(51)=(1)/(2)+(26)/(102) = (51)/(102)+(26)/(102)=(77)/(102)`

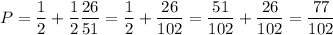
***NOTE!!!***

What I just wrote is the probability of picking exactly one spade/heart. In fact, as you can see, if I pick a spade/heart with the first pick, the game ends. If you meant "what are the odds of picking at least one spade/heart, then the answer is simply

`(26)/(52)(26)/(51)`

Because you have 26 "good" cards out of 52 possible cards with the first pick, and 26 "good" cards out of the remaining 51 if the first pick wasn't a spade nor a heart.