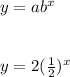Answer:
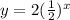
Explanation:
Given the exponential function as
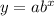
substitute both points in the equation above
point (-3,16) will be
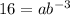
point (-1,4) will be
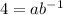
make a the subject of the formula in both equations above

This means
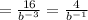
Cross multiply as;
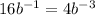
Divide by 4 both sides to get
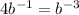
Divide by b^-1 both sides

Find value of a
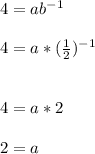
Hence
a=2 and b=1/2 thus write the equation as;