Question

Which is the equation of a parabola with a directrix at y = −3 and a focus at (−2, 3

Answer 1

Answer:
`y=(1)/(12)(x+2)^2`

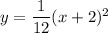
Explanation:

The vertex form of a parabola is: y = a(x - h)² + k where

• (h, k) is the vertex
• 
  `a=(1)/(4p)`

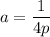
NOTE: p is the distance from the vertex to the focus.

The vertex is the midpoint between the focus and the directrix, so the vertex (h, k) = (-2, 0)

the distance from the vertex (-2, 0) to the focus (-2, 3) is 3 so p = 3

`a = (1)/(4(3))=(1)/(12)`

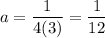
Insert (h. k) = (-2, 0) and a = 1/12 into vertex form to get:

`y = (1)/(12)[x- (-2)]^2+0\quad \implies \quad \boxed{y=(1)/(12)(x+2)^2}`