Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.

Quadrilateral JKLM has vertices J(8, 4), K(4, 10), L(12, 12), and M(14, 10). Match each quadrilateral, described by its vertices, to the sequence of transformations that will show it is congruent to quadrilateral JKLM.

Answer 1

1. W(5,1),X(1,7),Y(9,9) and Z(11,7).

2.A(-8,-4),B(-4,-10),C(-12,-12) and D(-14,-10).

3. E(5,6) ,F(1,12),G(9,14) and H(11,12).

4.O(10,1),P(6,7),Q(14,9) and R(16,7).

Explanation:

We are given that a quadrilateral JKLM with vertices J(8,4),K(4,10),L(12,12) and M(14,10)

We have to match a quadrilateral with its correct transformation of given quadrilateral JKLM

1.a transformation 3 units down and 3 units left

By using transformation rule
`(x,y)\rightarrow (x-3,y-3)`

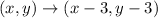
The new vertices of quadrilateral is (5,1), (1,7),(9,9) and (11,7).

Hence, the quadrilateral WXYZ with vertices W(5,1),X(1,7),Y(9,9) and Z(11,7).

2.A sequence of reflection across x- axis and y-axis in order

Reflection across x- axis

The transformation rule
`(x,y)\rightarrow (x,-y)`

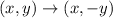
By using this rule

The vertices of quadrilateral are (8,-4),(4,-10),(12,-12) and (14,-10).

After the reflection across y- axis

The transformations rule

`(x,y)\rightarrow (-x,y)`

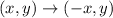
By using this rule

We get the new vertices of quadrilateral are (-8,-4),(-4,-10),(-12,-12) and (-14,-10).

Hence, the quadrilateral ABCD with vertices A(-8,-4),B(-4,-10),C(-12,-12) and D(-14,-10).

3.a translation 3 unit left and 2 units up

The transformation rule
`(x,y)\rightarrow (x-3,y+2)`

By using this rule

The new vertices are (5,6),(1,12),(9,14) and (11,12).

Hence, the quadrilateral EFGH with vertices E(5,6) ,F(1,12),G(9,14) and H(11,12).

4.a translation 2 units right and 3 units down

The transformation rule

`(x,y)\rightarrow (x+2,y-3)`

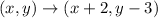
By using this rule

The new vertices are (10,1),(6,7),(14,9) and (16,7)

Hence, the quadrilateral OPQR with vertices O(10,1),P(6,7),Q(14,9) and R(16,7).