Answer:
43.531
Explanation:
This problem needs the law of cosines since the three sides of the triangle are involved as well as one angle. The law of cosines is:
c^2 = a^2 + b^2 - 2ab*cos(C)
Where the lowercase letters are side values and capital letters are angle values. Just in case I will mention side a is the one with a length of 14, side b is 20 and c = 12.
Since it is asking for angle A instead of angle C we can rewrite the law of cosines to fit that, basically just rearranging the letters.
a^2 = c^2 + b^2 - 2cb*cos(A)
Now we just plug in and solve.
14^2 = 12^2 + 20^2 - 2*12*20*cos(A)
Rearrange to get A by itself
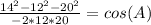
Now we take the inverse cosine, or arccos of both sides to get our answer.
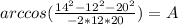
Let me know if there is something in my explanation you don't understand.