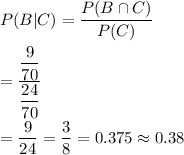Question

Please Hurry!!
Consider the two-way table below.
Find P(BIC).

Answer 1

Answer: the answer is B, or P(B|C)=9/24=0.38

Explanation:

If you look at the table, you can see that 9 is where BC is. So, 9 is the numerator. The denominator is 24 because that is the total number.

Also, I got this answer correct on Edge

Answer 2

Answer:
`P(B|C)=(9)/(24)=0.38`

Explanation:

The formula for conditional probability :-

`P(M|N)=(P(M\cap N))/(P(N))`

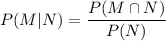
From the given table it can be seen that ,

Total = 70

`n(C)=24`

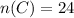
Then , the probability of having B:-

`\text{P(C)}=\frac{\text{n(C)}}{\text{Total}}\\\\=(24)/(70)`

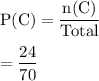
Also,
`n(B\cap C)=9`

Then , the probability of having the intersection of B and C :-

`P(B\cap C)=\frac{n(B\cap C)}{\text{Total}}\\\\=(9)/(70)`

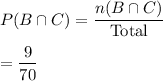
Then , by the formula of conditional probability , we have :-

`P(B|C)=(P(B\cap C))/(P(C))\\\\=((9)/(70))/((24)/(70))\\\\=(9)/(24)=(3)/(8)=0.375\approx0.38`