Question

Which best describes the transformation that occurs from

the graph of f(x) = x2 to g(x) = (x - 2)2 + 3?
right 2, up 3
left 2, down 3
right 2, down 3
left 2, up 3

Answer 1

It would be right 2, up three since whatever is in the parenthesis is the opposite of what you would think it is but the outside number of positive goes up but if negative goes down

Answer 2

A. right 2, up 3

Explanation:

We are asked to find the transformation that occurs from the graph of
`f(x)=x^2` to
`f(x)=(x-2)^2+3`.

Let us recall transformation rules:

`f(x)\rightarrow f(x+a)=\text{Graph shifted to left by a units}`

`f(x)\rightarrow f(x-a)=\text{Graph shifted to right by a units}`

`f(x)\rightarrow f(x)-a=\text{Graph shifted downwards by a units}`

`f(x)\rightarrow f(x)+a=\text{Graph shifted upwards by a units}`

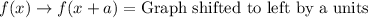
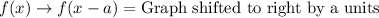
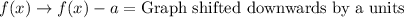
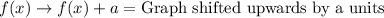
Upon looking at our given functions, we can see that graph of
`f(x)=x^2` is shifted to right by 2 units as 2 is inside parenthesis. The graph is shifted upwards by 3 units as we have positive 3 outside parenthesis.

Therefore, option A is the correct choice.