Answer:
x = 1, -1 + i, and -1 - i are the 3 roots
Explanation:
The Rational Root Theorem will help us find any real roots in this 3rd degree polynomial. The c value in that polynomia is -2 and the d value is 1 (the leading coefficient).
If c is -2, then the factors of -2 are:
1, -1, 2, -2
If d is 1, then the factors of 1 are:
1, -1
And c/d gives us all the possible roots:
1/1, -1/1, 2/1, -2/1 which of course simplify to
1, -1 2, -2
We will now use synthetic division to find the first real root. I will use x = 1 first.
For synthetic division:
1| 1 1 0 -2
is how it is set up. Bring down the first number, 1, multiply it by 1 and put that product up under the second "1":
1| 1 1 0 -2
1
1
Now add to get
1| 1 1 0 -2
1
1 2
Multiply 2 by 1 and put that product up under the 0 and add:
1| 1 1 0 -2
1 2
1 2 2
Again multiply the 2 by 1 and put that product up undeer the -2 and add:
1| 1 1 0 -2
1 2 2
1 2 2 0
That remainder of 0 tells us that x = 1 is a root of that polynomial and the depressed polynomial, made up from the bold numbers, is one degree less than what it started with:

This does not factor without imaginary roots, so putting it into the quadratic formula looks like this:
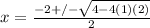
which simplifies to
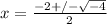
The square root of -4 simplifies to 2i, so

which reduces to
x = -1 + i and
x = -1 - i