Question

Charles has collected data to find that the total snowfall per year in Reamstown has a normal distribution. Using the Empirical Rule, what is the probability that in a randomly selected year, the snowfall was less than 87 inches if the mean is 72 inches and the standard deviation is 15 inches? Provide the final answer as a percent.

Answer 1

Explanation:

Correct answers:

84%

Notice that 87 inches is one standard deviation greater than the mean. Based on the Empirical Rule, 68% of the yearly snowfalls are within one standard deviation of the mean. Since the normal distribution is symmetric, this implies that 16% of the yearly snowfalls are greater than one standard deviation above the mean. Alternatively, 84% of the yearly snowfalls are less than one standard deviation above the mean.

Answer 2

0.8413 or 84.13%

Explanation:

Given : The mean is 72 inches and the standard deviation is 15 inches

To Find : What is the probability that in a randomly selected year, the snowfall was less than 87 inches

Solution:

Mean =
`\mu = 72`

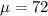
Standard deviation =
`\sigma = 15`

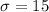
Formula :
`z=(x-\mu)/(\sigma)`

We are supposed to find the probability that in a randomly selected year, the snowfall was less than 87 inches

So, x = 87

Substitute the values in the formula

`z=(87-72)/(15)`

`z=1`

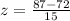
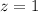
Now to find P(z<87) refer the z table

P(Z<87)=0.8413 = 84.13%

So, the probability that in a randomly selected year, the snowfall was less than 87 inches if the mean is 72 inches and the standard deviation is 15 inches is 0.8413 or 84.13%