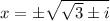Question

Find the solution of

X^4-2sqrt(3)X^2+4 = 0

Answer 1

see below

Explanation:

The four solutions are all complex.

The equation can be written in vertex form as ...

(x^2 -√3)^2 +1 = 0

This has solutions ...

x^2 -√3 = ±√-1 . . . . . . . . . . . . . . subtract 1, take the square root

x² = √3 ± i = 2∠±30° . . . . . . . . write in polar form to simplify root taking*

This has solutions for x ...

x = ±√(2∠±30°) = (±√2)∠±15° . . . . in polar form

x = ±√2(cos(15°) ± i·sin(15°)) . . . . . two conjugate pairs of solutions, total

x ≈ ±1.3660254 ±0.3660254i

_____

* We prefer not to have a complex number under a radical, as in ...

`x=\pm\sqrt{√(3)\pm i}`