Question

Find the inverse laplace transform of: (2 s + 4) / (s - 3)^3

Answer 1

`e^(3t)(2t+5t^(2))`

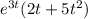
Explanation:

`L^(-1)[(2s+4)/((s-3)^(3)) ]=`

Using the Translation theorem to transform the s-3 to s, that means multiplying by and change s to s+3

Translation theorem:
`L^(1) [F(s-a)=L^(-1)[F(s)|_(s \to s-a)\\ L^(1) [F(s-a)=e^(at) f(t)`

`L^(-1)[(2s+4)/((s-3)^(3)) ]=e^(3t) L^(-1)[(2(s+3)+4)/(s^(3)) ]`

Separate the fraction in a sum:

`e^(3t) L^(-1)[(2s+10)/(s^(3)) ]=e^(3t) L^(-1)[(2s)/(s^(3))+(10)/(s^(3)) ]=e^(3t) (L^(-1)[(2)/(s^(2))]+ L^(-1)[(10)/(s^(3))])`

The formula for this is:

`L^(-1)[(n!)/(s^(n+1)) ]=t^(n)`

Modify the expression to match the formula.

`e^(3t) (2L^(-1)[(1)/(s^(1+1))]+ (10)/(2) L^(-1)[(2)/(s^(2+1))])=e^(3t) (2L^(-1)[(1)/(s^(1+1))]+ 5 L^(-1)[(2)/(s^(2+1))])`

Solve

`e^(3t) (2L^(-1)[(1)/(s^(1+1))]+ 5 L^(-1)[(2)/(s^(2+1))])=e^(3t)(2t+5t^(2) )`