Answer:
1.49
Explanation:
In order to find the slope of the tangent line to a given equation, and in a given point, we need to:
1. Find the first derivative of the given function.
2. Evaluate the first derivative function in the given point.
1. Let's find the first derivative of the given function:
The original function is
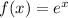
But remeber that the derivative of
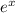 is
is
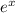
so,
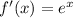
2. Let's evaluate the first derivative function in the given point
The given point is (0.4,1.49) so:
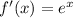

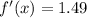
Notice that the calculated slope of the tangent line is equal to the y-coordinate of the given point because f'(x)=f(x). In conclusion, the slope of the tangent line is equal to 1.49.