Question

A simple random sample of 25 filtered 100mm cigarettes is obtained, and the tar content of each cigarette is measured. The sample has a mean 20.2mg and a standard deviation of 3.21mg. Use 0.05 significance level to test the claim that the mean tar content of filtered 100mm cigarettes is less then 21.1mg, which is the mean for unfiltered king size cigarettes. What do the results suggest, if anything about the effectiveness of the filters?

A) What is the test Statistic? = ____ Round to 2 decimal places
B) What is the critical Values= ___ Round to 2 decimal places as needed, Use a comma to separate answers as needed
C) What is the P-Value = ___ Round to four decimal places as needed

Answer 1

A) -1.40

B) -1.71

C) 0.0872

Explanation:

Sample size = n = 25

Sample mean = x = 20.2 mg

Sample standard deviation = s = 3.21 mg

Claim: Sample mean is less than 21.1 mg

So, u = 21.1

Null Hypothesis: u ≥ 21.1 mg

Alternate Hypothesis? u < 21.1 mg

Since we have the sample standard deviation, we will use the t-distribution to answer this question

Part A) t-test statistic

The formula to calculate the t-test statistic is:

`t=(x-u)/((s)/(√(n) ) )`

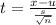
Using the values, we get:

`t=(20.2-21.1)/((3.21)/(√(25) ) )\\\\ t=-1.40`

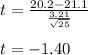
Thus, the value of t-test statistic is -1.40

Part B) Critical Value

In order to calculate the critical value we need the value of significance level and the number of degrees of freedom.

Degrees of freedom = df = n -1 = 25 - 1 = 24

Using t-table or t-critical value calculator for significance level 0.05 and 24 df the value comes out to be:

t-critical = -1.71

Since this is a left tailed test, we have considered the negative t-critical value. Rejection region will be the values less than -1.71 i.e. values which lie to left of -1.71

Part C) P-value

In order to calculate the P-value we need the t-score which we calculated in part A and the degrees of freedom.

Using the t-table or p value calculator the p value for t score of -1.40 and df 24 comes out to be:

p-value = 0.0872

Conclusion:

Since the p-value is larger than the significance level, we fail to reject the claim.

Also the test-statistic does not lie in the rejection region, so another hint that we cannot reject the claim.

Thus, no conclusion can be drawn about the effectiveness of the filters using these tests.