Question

Find the coordinates of the vertex for the parabola defined by the given quadratic function f(x) = (x + 2)^2 + 2 a) (0,2) b) (2.0) c) (-2.2) d) (-2,-2) e) none

Answer 1

(-2,2)

Explanation:

Let's find the answer.

Because a tangent line for a parabola function is equal to 0 only at its vertex then:

`f(x)=(x+2)^(2)+2`

`f'(x)=2*(x+2)`

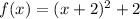
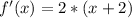
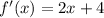`f'(x)=2x+4` so then:

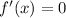`f'(x)=0` when

`0=2x+4`

`-2=x`

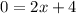
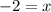
For x=-2 f(x) is:

`f(x)=(x+2)^(2)+2`

`f(1)=(-2+2)^(2)+2`

`f(x)=2`

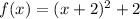
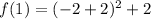
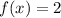
In conclusion, the vertex of the given parabola is (-2,2), so the answer is C. Although in your answer is reported as (-2.2) but I think was a typing mistake.