Answer:
The LCD is 72; the sum is 35/72
Explanation:
Let's find the least common denominator (LCD) and find a solution.
The given expression:
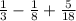has three fractions from which their denominators can be expressed as the multiplication of prime numbers:
Fraction 1: 1/3 --> 3 is a prime number
Fraction 2: 1/8 --> 8=2*4=2*2*2
Fraction 3: 5/18 --> 18=3*6=3*2*3
Now, the next step is considering that if a number is repeated using two different fractions, one of the numbers is deleted. Notice that 'fraction 1' has a 3 and 'fraction 3' also has a 3, so we delete one '3'. Now notice that 'fraction 2' has a 2 and 'fraction 3' also has a 2, so we delete one '2'. So initially we have:
(3)*(2*2*2)*(3*2*3)
But after the previous process (erasing one '3' from the first fraction and one '2' from the second fraction) we now have:
(2*2)*(3*2*3)
Doing the math we obtain (2*2)*(3*2*3)=72, so 72 is our LCD.
Now we have to multiply each fraction in order to obtain the same denominator (LCD=72) for all fractions, so:
For fraction 1: 1/3 --> (1/3)*(24*24)=24/72
For fraction 2: 1/8 --> (1/8)*(9/9)=9/72
For fraction 3: 5/18 --> (5/18)*(4/4)=20/72
Now we can sum all the fractions (remember the correct sign for each fraction):
24/72 - 9/72 + 20/72 = (24-9+20)/72 = 35/72