Answer:
Bisection method for x=3 as the answer
Explanation:
Let's find an answer using the bisection method.
Because the problem gave us a valid bracket, we can establish that 'x', with a value between 1.8 and 5.1, is a solution for the equation, but let's understand why:
The equation
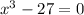 can be written as:
can be written as:
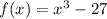 then:
then:
If
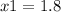 and
and
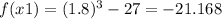
If
 and
and
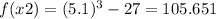
Notice that the results are different in sign, the first one is negative whereas the second one is positive, meaning that there is a value (x) between them which permits f(x)=0, which in other words means that there is a root between 1.8 and 5.1.
The bisection method uses the mid-point (m) in each interaction between the two numbers defining the bracket (a,b), so:
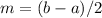 which in our case is:
which in our case is:
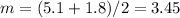 and
and
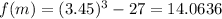
Notice that the result is positive but lesser than 105.651 from using x2, so now we change the bracket from (1.8,5.1) to (1.8,3.45) and we apply the method again:
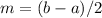 which in our case is:
which in our case is:
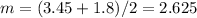 and
and
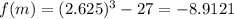
Notice that now the result is negative but higher than -21.168 obtained from using x1, so now we change the bracket from (1.8,3.45) to (2.625,3.45). After this we apply the method again and again using the same estructure until we obtain a 'm' value from which f(m)=0, like this:
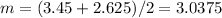 and
and
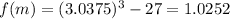
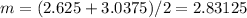 and
and
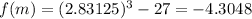
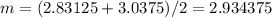 and
and
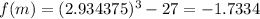
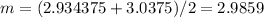 and
and
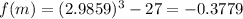
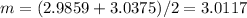 and
and
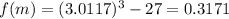
 and
and
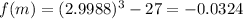
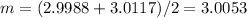 and
and
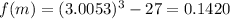
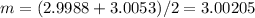 and
and
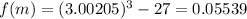
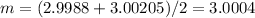 and
and
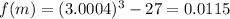
 and
and
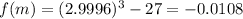
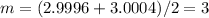 and
and
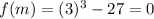
Finally look that f(m)=0, so the root is x=3.