Question

Find all the solutions for the equation:

2y2 dx - (x+y)2 dy=0

(Introduction to Differential Equations)

Answer 1

`2y^2\,\mathrm dx-(x+y)^2\,\mathrm dy=0`

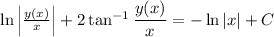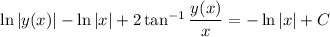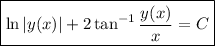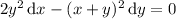
Divide both sides by
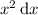`x^2\,\mathrm dx` to get

`2\left(\frac yx\right)^2-\left(1+\frac yx\right)^2(\mathrm dy)/(\mathrm dx)=0`

`(\mathrm dy)/(\mathrm dx)=(2\left(\frac yx\right)^2)/(\left(1+\frac yx\right)^2)`

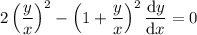
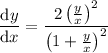
Substitute
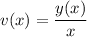`v(x)=\frac{y(x)}x`, so that
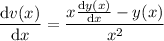`(\mathrm dv(x))/(\mathrm dx)=(x(\mathrm dy(x))/(\mathrm dx)-y(x))/(x^2)`. Then

`x(\mathrm dv)/(\mathrm dx)+v=(2v^2)/((1+v)^2)`

`x(\mathrm dv)/(\mathrm dx)=(2v^2-v(1+v)^2)/((1+v)^2)`

`x(\mathrm dv)/(\mathrm dx)=-(v(1+v^2))/((1+v)^2)`

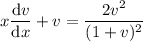
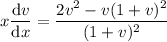
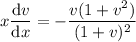
The remaining ODE is separable. Separating the variables gives

`((1+v)^2)/(v(1+v^2))\,\mathrm dv=-\frac{\mathrm dx}x`

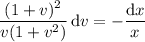
Integrate both sides. On the left, split up the integrand into partial fractions.

`((1+v)^2)/(v(1+v^2))=(v^2+2v+1)/(v(v^2+1))=\frac av+(bv+c)/(v^2+1)`

`\implies v^2+2v+1=a(v^2+1)+(bv+c)v`

`\implies v^2+2v+1=(a+b)v^2+cv+a`

`\implies a=1,b=0,c=2`

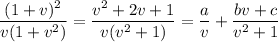
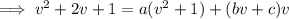
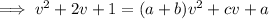
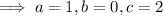
Then

`\displaystyle\int((1+v)^2)/(v(1+v^2))\,\mathrm dv=\int\left(\frac1v+\frac2{v^2+1}\right)\,\mathrm dv=\ln|v|+2\tan^(-1)v`

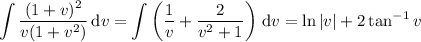
On the right, we have

`\displaystyle-\int\frac{\mathrm dx}x=-\ln|x|+C`

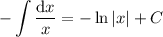
Solving for
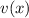`v(x)` explicitly is unlikely to succeed, so we leave the solution in implicit form,

`\ln|v(x)|+2\tan^(-1)v(x)=-\ln|x|+C`

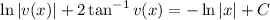
and finally solve in terms of
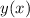`y(x)` by replacing
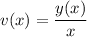`v(x)=\frac{y(x)}x`:

`\ln\left|\frac{y(x)}x\right|+2\tan^(-1)\frac{y(x)}x=-\ln|x|+C`

`\ln|y(x)|-\ln|x|+2\tan^(-1)\frac{y(x)}x=-\ln|x|+C`

`\boxed{\ln|y(x)|+2\tan^(-1)\frac{y(x)}x=C}`