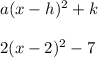Question

What is the vertex form of y=2x^2-8x+1

Answer 1

`2(x-2)^2-7`

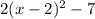
Explanation:

`y=2x^2-8x+1`

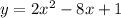
When comparing to standard form of a parabola:
`ax^2+bx+c`

• 
  `a=2`
• 
  `b=-8`
• 
  `c=1`

Vertex form of a parabola is:
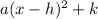`a(x-h)^2+k`, which is what we are trying to convert this quadratic equation into.

To do so, we can start by finding "h" in the original vertex form of a parabola. This can be found by using:
`(-b)/(2a)`.

Substitute in -8 for b and 2 for a.

`(-(-8))/(2(2))`

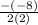
Simplify this fraction.

`(8)/(4) \rightarrow2`

`\boxed{h=2}`

The "h" value is 2. Now we can find the "k" value by substituting in 2 for x into the given quadratic equation.

`y=2(2)^2-8(2)+1`

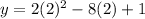
Simplify.

`y=-7`

`\boxed{k=-7}`

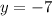
We have the values of h and k for the original vertex form, so now we can plug these into the original vertex form. We already know a from the beginning (it is 2).

`a(x-h)^2+k\\ \\ 2(x-2)^2-7`