Question

A nonconducting sphere contains positive charge distributed uniformly throughout its volume. Which statements about the potential due to this sphere are true? All potentials are measured relative to infinity. (There may be more than one correct choice)

a) The potential is highest at the center of the sphere. b) The potential at the center of the sphere is the same as the potential at the surface. c) The potential at the surface is higher than the potential at the center. d) The potential at the center is the same as the potential at infinity. e) The potential at the center of the sphere is zero.

Answer 1

a). The potential is highest at the center of the sphere

Step-by-step explanation:

We k ow the potential of a non conducting charged sphre of radius R at a point r < R is given by

`E=\left [ (K.Q)/(2R) \right ]\left [ 3-((r)/(R))^(2) \right ]`

Therefore at the center of the sphere where r = 0

`E=\left [ (K.Q)/(2R) \right ]\left [ 3-0 \right ]`

`E=\left [ (3K.Q)/(2R) \right ]`

Now at the surface of the sphere where r = R

`E=\left [ (K.Q)/(2R) \right ]\left ( 3-1 \right )`

`E=\left [ (2K.Q)/(2R) \right ]`

`E=\left [ (K.Q)/(R) \right ]`

Now outside the sphere where r > R, the potential is

`E=\left [ (K.Q)/(r) \right ]`

This gives the same result as the previous one.

As
`r\rightarrow \infty , E\rightarrow 0`

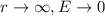
Thus, the potential of the sphere is highest at the center.