Answer:
x=2, x=1, x=-5 and x=-3.
Explanation:
Let's find the answer using the following method.
Original equation:
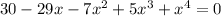
Notice that the constant term is 30, which can be divided by:
1, -1, 2, -2, 3, -3, 5, -5, 6, -6, 10, -10, 15, -15, 30, -30.
Trying this divisors can allowed us to find one or even two initial roots, so:
Trying first x=1, we have:
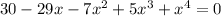
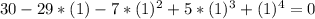
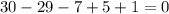
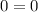 notice that x=1 is a root.
notice that x=1 is a root.
Let's try now with x=2, we have:
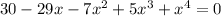
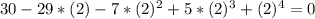
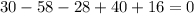
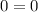 notice that x=2 is also a root.
notice that x=2 is also a root.
So the original equation can be written as:
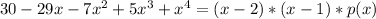 so:
so:
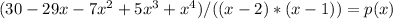
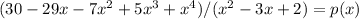
Doing the math, we have:
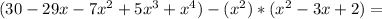
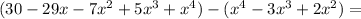
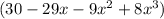 now:
now:
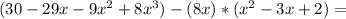
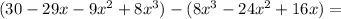
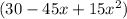 now:
now:
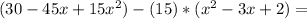
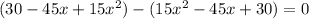
which means:
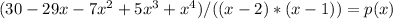
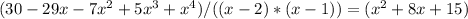
Using the equation for calculating the roots of a quadratic equation we have:
quadratic equation:
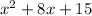
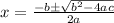
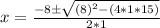
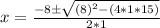
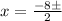
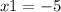
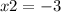
So finally we have:
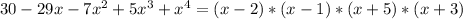
In conclusion the roots are: x=2, x=1, x=-5 and x=-3.