Question

Last year Carson Industries issued a 10-year, 12% semiannual coupon bond at its par value of $1,000. Currently, the bond can be called in 6 years at a price of $1,060 and it sells for $1,200. What are the bond's nominal yield to maturity and its nominal yield to call? Do not round intermediate calculations. Round your answers to two decimal places.

Answer 1

YTM = 8.93%

YTC = 8.47%

Step-by-step explanation:

`P = (C)/(2) *(1-(1+YTC/2)^(-2t) )/(YTC/2) + (CP)/((1+YTC/2)^(2t))`

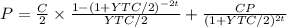
The first part is the present value of the coupon payment until the bond is called.

The second is the present value of the called amount

P = market price value = 1,200

C = annual coupon payment = 1,000 x 12% 120

C/2 = 60

CP = called value = 1,060

t = time = 6 years

`P = 60 *(1-(1+YTC/2)^(-2* 6) )/(YTC/2) + (1,060)/((1+YTC/2)^(2* 6))`

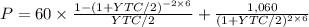
Using Financial calculator we get the YTC

8.467835879%

`P = 60 *(1-(1+YTM/2)^(-2* 10) )/(YTM/2) + (1,000)/((1+YTM/2)^(2* 10))`

The first part is the present value of the coupon payment until manurity

The second is the present value of the redeem value at maturity

P = market price value = 1,200

C = coupon payment = 1,000 x 12%/2 = 60

C/2 = 60

F = face value = 1,060

t = time = 10 years

Using Financial calculator we get the YTM

8.9337714%