Answer:
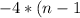 with n=1,2.3,4....
with n=1,2.3,4....
Explanation:
the sequence is 3, -12, 48, -192,...
This the negative in every second term indicates that the previous term is multiplied by negative number. We can also determine the common factor by taking -12, 48, 192 and dividing them by 4, therefore we will get the previous term. If we mutliply the 3 with -4 we get -12, if we multiply -12 with -4 we get 48, if we mutliply 48 by -4 we get -192 and so forth.
The recursive rule if n is the first term is:
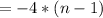
with n=1,2,3, ...