Question

Solve and graph the absolute value inequality: |2x + 4| > 8. number line with open circles on negative 6 and 2, shading in between. number line with closed circles on negative 6 and 2, shading going in the opposite directions. number line with open circles on negative 6 and 2, shading going in the opposite directions. number line with open circles on negative 2 and 2, shading going in the opposite directions.

Answer 1

Part 1) The solution of the absolute value is (-∞,-6)∪ (2,∞)

Number line with open circles on negative 6 and 2, shading going in the opposite directions

Part 2) The graph in the attached figure

Explanation:

we have

`\left|2x+4\right|>8`

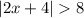
we know that

The absolute value has two solutions

step 1

Find the positive case

`+(2x+4)>8`

`2x>8-4`

`2x>4`

`x>2`

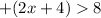
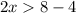
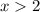
The solution is the interval ----> (2,∞)

All real numbers greater than 2

step 2

Find the negative case

`-(2x+4)>8`

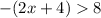
Multiply by -1 both sides

`(2x+4)<-8`

`2x<-8-4`

`2x<-12`

`x< -6`

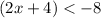
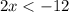
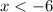
The solution is the interval ----> (-∞,-6)

All real numbers less than -6

therefore

The solution of the absolute value is

(-∞,-6)∪ (2,∞)

Number line with open circles on negative 6 and 2, shading going in the opposite directions

step 3

using a graphing tool

see the attached figure