Question

Compute the entry (the number in the second row and second column) of the product matrix resulting from the following multiplication:

[1 2] [9 6]
[3 4] [5 7]

Answer 1

The entry on the second row and second column of the product matrix is
`c_(22) = 40`.

Explanation:

Let's define as A and B the given matrixes:

`A = \left[\begin{array}{cc}1&2\\3&4\end{array}\right]`

`B = \left[\begin{array}{cc}9&6\\5&7\end{array}\right]`

The product matrix C entry in the first row and first column
`c_(1,1)` or
`c_(11)` can be computer multiplying first row of A by first column of B (see example attached).

The product matrix C entry in the first row and second column
`c_(1,2)` or
`c_(12)` can be computer multiplying first row of A by second column of B.

The product matrix C entry in the second row and first column
`c_(2,1)` or
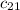`c_(21)` can be computer multiplying second row of A by first column of B.

The product matrix C entry in the second row and second column
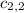`c_(2,2)` or
`c_(22)` can be computer multiplying second row of A by second column of B.

Then, let's compute
`c_(22)` by doing the dot product between [3 4] and [6 7]...

`c_(22) = [3 4] . [6 7] = 3*4 + 4*7 = 12 + 28 = 40`