Question

Suppose medical records indicate that the length of newborn babies(in inches) is normally distributed with a mean of 20 and a standard deviation of 2.6 find the probability that a given infant is between 14.8 and 25.2 inches long

Answer 1

95%

Explanation:

Answer 2

P=0.954 or 95.4%

Explanation:

Using the formula for the standardized normal distribution to find Z:

`Z=(X-\mu)/(\sigma)`

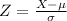
Where μ is the mean (μ=20) and σ is the standard deviation (σ=2.6).

`Z_(1) =(14.8-20)/(2.6)=-2.0`

`Z_(1) =(25.2-20)/(2.6)=2.0`

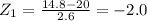
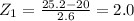
In the table of the normal distribution, we can look for positive values z, and these values are going to represent the area under the curve between z=0 and the values searched. the negatives values are found by symmetry (with the corresponding positive value but remember this area is under the left side of the curve). To find a value in the table, find the units in the first column and the follow over the same row till you find the decimals required.

`P_1=0.4772`

`P_2=0.4772`

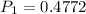
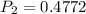
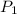`P_1` represents the probability of length being between 14.8 and 20 (the mean) and
`P_2` represents the probability of length being between 20 and 25.2, The requested probability is the sum of these two.

`P=P_1+P_2=0.954`