Answer:
-5
Explanation:
Let's find the answer by dividing
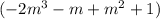 by
by
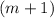 , like this:
, like this:
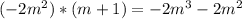 and:
and:
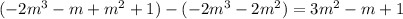 then:
then:
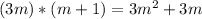 and:
and:
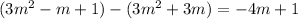 then:
then:
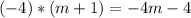 and:
and:
 notice that the remainder is 5 so we need to subtract the remainder.
notice that the remainder is 5 so we need to subtract the remainder.
Based on the previous procedure we can define:
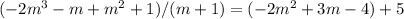
In conclusion the smallest integer that can be added to the polynomial is -5, so the polynomial will be
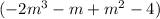 .
.