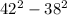Question

Which shows 42^2 − 28^2 being evaluated using the difference of perfect squares method?

422 − 382 = (1,764 − 1,444)(1,764 + 1,444) = 1,283,200

422 − 382 = 1,764 − 1,444 = 400

422 − 382 = (42 − 38)2 = (4)2 = 16

422 − 382 = (42 + 38)(42 − 38) = (70)(4) = 280

Answer 1

None

Explanation:

The general form of the difference of perfect squares method is:
`a^2-b^2=(a+b)(a-b)`

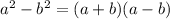
Demonstration

The right part of the previous equation could be split like this:

`a^2-b^2=a^2-a\cdot b + a\cdot b - b^2`

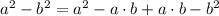
Which can be simplified like this:

`a^2-b^2=a^2-b^2`

We have obtained the same result

Real problem

According to the problem
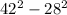`42^2 - 28^2` the development would be:

`42^2 - 28^2=(42+28)\cdot (42-28)`

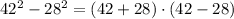
The idea is to solve each pair of parenthesis and then to multiply.

`42^2 - 28^2=(70)\cdot (14)=980`

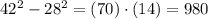
Thus, the result is not in the options because the problem asks for
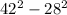`42^2 - 28^2` and the options are related to
`42^2 - 38^2`

Answer 2

`42^(2) -28^(2) =980`

Explanation:

If you evaluate the equation using the factorization method by difference of perfect squares, it would be done as follows

`a^(2) -b^(2)  = (a+b)(a-b)`

Therefore

`42^(2) -28^(2)   =   (42-28)(42+28)`

Solving

`(14)(70)=980`