Question

According to Bernoulli's equation, the pressure in a fluid will tend to decrease if its velocity increases. Assuming that a wind speed of 1 m/s causes a pressure drop of 0.645 Pa, what pressure drop is predicted by Bernoul's equation for a wind speed of 5 m/s? Multiple Choice 3.325 Pa 129 Pa 194 Pa 16 125 Pa

Answer 1

16.125 Pa

Step-by-step explanation:

The Bernoulli equation despising the height changes is:

`(P_(2)-P_(1))/(pg)+((v_(2)^(2)-v_(1)^(2))/(2g))=0`

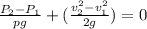
The gravity constant can be cancelled.

Applying the equation to the first situation,
`v_(1)=0` ,
`v_(2)=1`,
`P_(2)-P_(1)=-0.645`

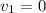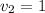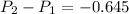
The density 'p' may be calculated because it is the only unknown.

`p=(-2(P_(2)-P_(1)))/(v_(2)^(2))=(-2*-0.645)/(1^(2))=1.29(kg)/(m^(3) )`

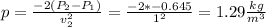
Applying the equation to the second situation, where the only unknown is the pressure drop (
`P_(2)-P_(1)`):

`P_(2)-P_(1)=-p*((v_(2)^(2)-v_(1)^(2))/(2))`

`P_(2)-P_(1)=-1.29*((5_(2)^(2))/(2))=-16.125`

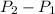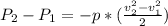
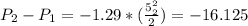
In both cases the assumption is
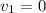`v_(1)=0` because its supposed that the air is stored.