Question

An investment project costs $10,000 and has annual cash flows of $2,920 for six years. a. What is the discounted payback period if the discount rate is zero percent? (Enter 0 if the project never pays back. Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) b. What is the discounted payback period if the discount rate is 4 percent? (Enter 0 if the project never pays back. Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) c. What is the discounted payback period if the discount rate is 21 percent?

Answer 1

(A) payback in 3.42 years

(B) It doesn't payback in six years. payback is 6.66 years

Step-by-step explanation:

(A) because discount rate is zero we are doing the payback period

`(investment)/(cashflow \: per \: year) = payback \: in \: years`

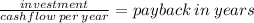
10000 investment / 2920 per year = 3.4246

(B) here there is a discount rate so we need to solve ussing the annuity formula for the time which makes the 2,920 cash flow equal to 10,000

`annuity * \frac{1 - {1 + rate}^( - time) }{rate} = principal`

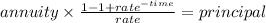
we post our givens in the formula

we pass the annuity and rate to the second part of the equation

`1 - {1.21}^( - time) = 10000 \: / 290 * .21`

10,000/2920*0.21= 0.7191...

for rounding porpuses I will refer to this as "a"

This means you have to work with the complete number, don't round it.

then, we work the equation a little more to reach this structure

`{1.21}^( - time) = 1 - a`

finally, we use log properties to solve for time

`(log (1 - a))/( log(1.21) ) = - 6.662638`

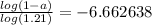
-time = -6.662638

time = 6.662638

But the project life is six years... so the project doesn't payback at this discount rate.