Question

Figure VWYX is a kite. What is the value of x?

Answer 1

The value of x is 6.

Explanation:

Given information: VWYX is a kite, ∠W=(18x-2)° and ∠X=(12x+2)°.

According to the properties of kite, the sum of opposite angles of a kite is 180°.

In kite VWYX, ∠W and ∠X are opposite angles, so their sum is 180°.

`\angle W+\angle X=180^(\circ)`

`(18x-2)+(12x+2)=180`

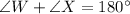
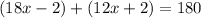
On combining like terms we get

`(18x+12x)+(-2+2)=180`

`30x=180`

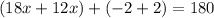
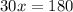
Divide both sides by 30.

`x=(180)/(30)`

`x=6`

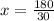
Therefore the value of x is 6.

Answer 2

For this case we have that by definition, the sum of the internal angles of a quadrilateral is 360 degrees.

So we have to:

`(18x-2) + (12x + 2) + 90 + 90 = 360`

In the figures they indicate that there are two angles of 90 degrees.

We eliminate parentheses:

`18x-2 + 12x + 2 + 90 + 90 = 360`

We add similar terms:

`18x + 12x-2 + 2 + 90 + 90 = 360\\30x + 180 = 360\\30x = 360-180\\30x = 180\\x = \frac {180} {30}\\x = 6`

Answer:

`x = 6`