Question

The polynomial function F(x) = 2x2 +8x-7 has a critical point at which of the

following x-values?
Oo oo
mio è
A. x=-7
B. x= -2
C. x= 0
D. x = 2

Answer 1

Option B
`x=-2`

Explanation:

we know that

The critical point of a function are the points on the graph of a function where the derivative is zero or the derivative does not exist.

we have

`f(x)=2x^(2)+8x-7`

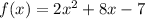
step 1

Take the derivative of the function

`f'(x)=4x+8`

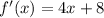
step 2

Set that derivative equal to 0 and solve for x. Each x value you find is known as a critical number

`f'(x)=0`

`4x+8=0`

`4x=-8`

`x=-2`

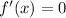
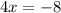
Alternative Method

The critical point of the quadratic equation is the vertex, because the function changes from decreasing to increasing at that point (In this problem the vertex is a minimum)

we have

`f(x)=2x^(2)+8x-7`

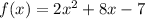
Convert into vertex form

`f(x)+7=2x^(2)+8x`

`f(x)+7=2(x^(2)+4x)`

`f(x)+7+8=2(x^(2)+4x+4)`

`f(x)+15=2(x^(2)+4x+4)`

`f(x)+15=2(x+2)^(2)`

`f(x)=2(x+2)^(2)-15`

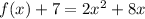
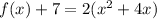
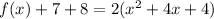
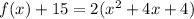
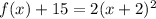
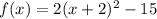
the vertex is the point (-2,-15)

therefore

The x-coordinate of the critical point is x=-2