Question

A rocket is launched upward so that its distance, in feet, above the ground after t seconds is represented by the function below. What is its maximum height? h(t) = -14t^2 +420t a) 13,020 ft b) 5684 ft c) 3150 ft d) 1740 ft e) none

Answer 1

The maximun height that the rocket will reach is 3150 ft.

Explanation:

This problem requieres that we maximize the function. For this we need the function to be of the form:

`f(x)=ax^2+bx+c`

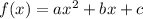
We already have that covered, as the height of the rocket is represented by:

`h(t)=-14t^2+420t`

We start calculating the derivative of h(t), wich is:

`h'(t)=-28t+420`

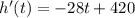
We need to remember that the derivative of a function represents the slope of said function at a given point. The maximum value of the function will have a slope equal to zero.

So we find the value in wich the derivative equals zero:

`0=-28t+420\\28t=420\\t=(420)/(28)\\t=15`

This means that 15 seconds is the time at wich the rocket will reach it's maximum height.

We replace this value in the original equation to solve the problem:

`h(15)=(-14)(15^2)+(420)(15)\\h(15)=-3150+6300\\h(15)=3150`

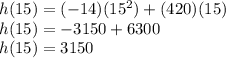
With this we can conclude that the maximum height the rocket will reach is 3150 ft.