Answer:
The two lengths are 3.4303 and 9.8606 centimeters
Explanation:
The metal bar is divided into two pieces, so we are going to call X the length of the first piece and Y the length of the second piece.
From the phrase: one piece is 3 centimeters longer than twice the length of the other, we can separate and rewrite as:
One piece - is - 3 centimeters - longer than - twice the length of the other
X = 3 + 2 * Y
So, X=3+2Y is our first equation
From the phrase: the sum of the squares of the two lengths is 109 square centimeters, we can rewrite as:
The sum of the squares of the two lengths - is - 109 square centimeters
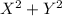 = 109
= 109
So, X^2+Y^2=109 is our second equation
Replacing the first equation on the second question we get:

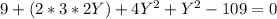
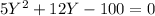
Solving this equation we find two solutions:
Y=3.4303 and Y= -5.8303
Since the question is talking about the length there is no sense use Y=-5.8303, then our first length is 3.4303
So replacing this value on the first equation we get:
X= 3 + 2*Y
X= 3 + 2*3.4303
X= 9.8606
Finally the two length are 3.4303 and 9.8606 centimeters