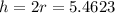Question

A cylindrical can has a volume of 128pi cm^3. What dimensions yield the minimum surface area? cm. The radius of the can with the minimum surface area is (Simplify your answer.) The height of the can with the minimum surface area is (Simplify your answer.) cm.

Answer 1

r=2.731 cm; h=5.462 cm

Explanation:

We are going to built a system of equations relating the radius 'r' and height 'h'. The first equation is the volume of a cylinder.

`V=\pi r^(2) h`

The problem requires to optimize the area, finding the minimum. The area of a cylinder is:

`2\pi rh+2\pi r^(2)=2\pi (r^(2) +rh)`

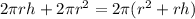
For the second and third equation we are going to use the Lagrange Multipliers method. This method is the optimization of a function of several variables with a restriction. In this case, the volume is the restriction:

`128=\pi r^(2) h`

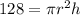
The function that we want to optimize is the Area, so applying the Lagrange method:

First, calculate the partial derivatives:

`A_(r)=2\pi (2r+h)`

`A_(h)= 2\pi r`

`V_(r)=2\pi rh`

`V_(h)=\pi r^(2)`

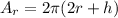
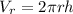
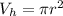
Then, the Lagrange multipliers method is formulated:

`(A_(r) ,A_(h) )=K(V_(r) ,V_(h))`

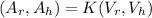
With the restriction

`128=\pi r^(2) h`

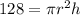
Our system of equation is:

Eq. 1
`2\pi (2r+h)=K2\pi rh\\ 2r+h=Krh`

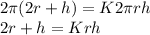
Eq. 2
`2\pi r=K\pi r^(2) \\ 2=Kr`

Eq. 3
`128=\pi r^(2) h`

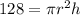
Replacing second equation in the first (replace the product
`Kr`)

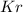Eq. 4
`2r+h=2h\\ 2r-h=0\\ h=2r`

Replacing this equation in third equation:

`128=\pi r^(2) (2r)=2\pi r^(3)`

At this point it is possible to calculate the radius:

`r=\sqrt[3]{(128)/(2\pi ) } =2.7311 cm`

The height is calculated with equation 4.

`h=2r=5.4623`