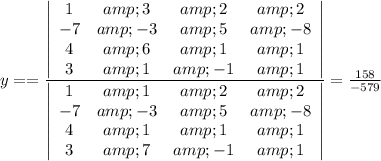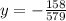Question

[10] In the following given system, determine a matrix A and vector b so that the system can be represented as a matrix equation in the form AX = b. In the given linear system, solve for y without solving for X, Z and w by using Cramer's rule, x + y + 2 + 2w = 3. -7x – 3y + 5z - 8w = -3 4x + y + z + w = 6 3x + 7y - Z + w = 1

Answer 1

`y=-(158)/(579)`

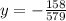
Explanation:

To find the matrix A, took all the numeric coefficient of the variables, the first column is for x, the second column for y, the third column for z and the last column for w:

`A=\left[\begin{array}{cccc}1&1&2&2\\-7&-3&5&-8\\4&1&1&1\\3&7&-1&1\end{array}\right]`

And the vector B is formed with the solution of each equation of the system:
`b=\left[\begin{array}{c}3\\-3\\6\\1\end{array}\right]`

To apply the Cramer's rule, take the matrix A and replace the column assigned to the variable that you need to solve with the vector b, in this case, that would be the second column. This new matrix is going to be called
`A_(2)`.

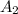`A_(2)=\left[\begin{array}{cccc}1&3&2&2\\-7&-3&5&-8\\4&6&1&1\\3&1&-1&1\end{array}\right]`

The value of y using Cramer's rule is:

`y=(det(A_(2)) )/(det(A))`

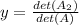
Find the value of the determinant of each matrix, and divide:

`y==\frac{\left|\begin{array}{cccc}1&3&2&2\\-7&-3&5&-8\\4&6&1&1\\3&1&-1&1\end{array}\right|}{\left|\begin{array}{cccc}1&1&2&2\\-7&-3&5&-8\\4&1&1&1\\3&7&-1&1\end{array}\right|} =(158)/(-579)`

`y=-(158)/(579)`