Question

1.(a) Find the matrix that represent the linear transformation f: p1\rightarrowp1 with respect to the bais {1,x};

f(a+bx)=(8a+2b)+(5a-b)x

(b) Does there exist a basis of P1 with respect to which f has a diagonal matrix that represents it? If so, what is the basis.

Answer 1

`a) \quad A=\left[\begin{array}{cc}8&5\\5&-1\end{array}\right] \\\\\\b) \quad \{-1+5x, 2+x\}`

Explanation:

To compute the representation matrix A of f with respect the basis {1,x} we first compute

`f(1)=f(1+0x)=(8\cdot 1 + 2 \cdot 0) + (5 \cdot 1 - 0)x=8+5x \\\\f(x)=f(0 + 1\cdot x)=(8 \cdot 0 + 2\cdot 1)+(5 \cdor 0 - 1)x = 2-1`

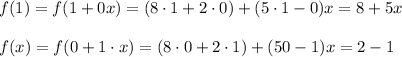
The coefficients of the polynomial f(1) gives us the entries of the first column of the matrix A, where the first entry is the coefficient that accompanies the basis element 1 and the second entry is the coefficient that accompanies the basis element x. In a similar way, the coefficients of the polynomial f(x) gives us the the entries of the second column of A. It holds that,

`A=\left[\begin{array}{ccc}8&5\\2&-1\end{array}\right]`

(b) First, note that we are using a one to one correspondence between the basis {1,x} and the basis {(1,0),(0,1)} of
`\mathbb{R}^2`.

To compute a basis P1 with respect to which f has a diagonal matrix, we first have to compute the eigenvalues of A. The eigenvalues are the roots of the characteristic polynomial of A, we compute

`0=\det\left[\begin{array}{ccc}8-\lambda & 2\\ 5 & -1-\lambda \end{array}\right]=(8 - \lambda)(-1-\lambda)-18=(\lambda - 9)(\lambda +2)`

and so the eigenvalues of the matrix A are
`\lambda_1=-2 \quad \text{and} \quad \lambda_2=9`.

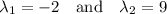After we computed the eigenvalues we use the systems of equations

`\left[\begin{array}{cc}8&2\\5&-1\end{array}\right]\left[\begin{array}{c}x_1\\x_2\end{array}\right] = \left[\begin{array}{c}-2x_1\\-2x_2\end{array}\right] \\\\\text{and} \\\\\left[\begin{array}{cc}8&2\\5&-1\end{array}\right]\left[\begin{array}{c}x_1 \\ x_2\end{array}\right]=\left[\begin{array}{cc}9x_1\\2x_1\end{array}\right]`

to find the basis of the eigenvalues. We find that
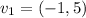`v_1=(-1,5 )` is an eigenvector for the eigenvalue -2 and that
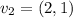`v_2=(2,1)` is an eigenvector for the eigenvalue 9. Finally, we use the one to one correspondence between the
`\mathbb{R}^2` and the space of liear polynomials to get the basis
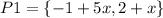`P1=\{-1+5x, 2+x\}` with respect to which f is represented by the diagonal matrix
`\left[\begin{array}{ccc}-2&0\\0&9\end{array}\right]`