Question

2. According to a medical study, it takes about 46.2 hrs, on average, for Roseola virus to fade away in infected patients (children). Assuming that the fading times of Roseola virus in infected patients have a nearly symmetric/bell-curve distribution with standard deviation 0.55, find the percent (%) of the cases where the fading time of the virus in an infected patient is less than 47.85 hours.

Answer 1

P(47.85 < x) = 0.9987

Explanation:

you must find the probability P(47.85 < x)

therefore, using the normal distribution:

finding z:

Z = (x-μ)/σ/() [1]

where:

x is the raw measurement

μ is the mean

σ is the standard deviation

n is the sample size

our information is:

μ = 46.2 hours, σ = 0.55 hours, n = 1, x = 47.85

so replacing:

`Z = ((47.85-46.2))/((0.55)/(√(1)))\\\\Z = (1.65)/(0.55)\\\\Z = (1.65)/(0.55)\\\\Z = 3\\\\`

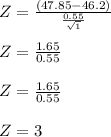
now you look at the normal distribution table and find Z score:

an this is 0.9987, you can check in the attached table.

so P(x<47.85) = 0.9987.or 99.87%