Question

Determine the exact formula for the following discrete models:

2tn+2 = 3tn+1 + 2tn; t0 = 1; t1 = 3;

49yn+2 = -16yn; y0 = 0; y1 = 2;

9xn+2 = 12xn+1- 85xn; x0 = 0; x1 =1

Answer 1

I'm partial to solving with generating functions. Let

`T(x)=\displaystyle\sum_(n\ge0)t_nx^n`

Multiply both sides of the recurrence by
`x^(n+2)` and sum over all
`n\ge0`.

`\displaystyle\sum_(n\ge0)2t_(n+2)x^(n+2)=\sum_(n\ge0)3t_(n+1)x^(n+2)+\sum_(n\ge0)2t_nx^(n+2)`

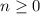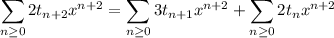
Shift the indices and factor out powers of
`x` as needed so that each series starts at the same index and power of
`x`.

`\displaystyle2\sum_(n\ge2)2t_nx^n=3x\sum_(n\ge1)t_nx^n+2x^2\sum_(n\ge0)t_nx^n`

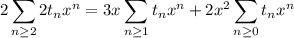
Now we can write each series in terms of the generating function
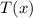`T(x)`. Pull out the first few terms so that each series starts at the same index
`n=0`.

`2(T(x)-t_0-t_1x)=3x(T(x)-t_0)+2x^2T(x)`

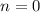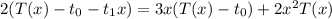
Solve for
`T(x)`:

`T(x)=(2-3x)/(2-3x-2x^2)=(2-3x)/((2+x)(1-2x))`

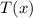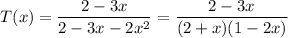
Splitting into partial fractions gives

`T(x)=\frac85\frac1{2+x}+\frac15\frac1{1-2x}`

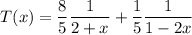
which we can write as geometric series,

`T(x)=\displaystyle\frac8{10}\sum_(n\ge0)\left(-\frac x2\right)^n+\frac15\sum_(n\ge0)(2x)^n`

`T(x)=\displaystyle\sum_(n\ge0)\left(\frac45\left(-\frac12\right)^n+\frac{2^n}5\right)x^n`

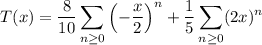
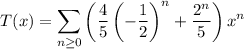
which tells us

`\boxed{t_n=\frac45\left(-\frac12\right)^n+\frac{2^n}5}`

# # #

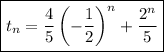
Just to illustrate another method you could consider, you can write the second recurrence in matrix form as

`49y_(n+2)=-16y_n\implies y_(n+2)=-(16)/(49)y_n\implies\begin{bmatrix}y_(n+2)\\y_(n+1)\end{bmatrix}=\begin{bmatrix}0&-(16)/(49)\\1&0\end{bmatrix}\begin{bmatrix}y_(n+1)\\y_n\end{bmatrix}`

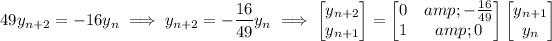
By substitution, you can show that

`\begin{bmatrix}y_(n+2)\\y_(n+1)\end{bmatrix}=\begin{bmatrix}0&-(16)/(49)\\1&0\end{bmatrix}^(n+1)\begin{bmatrix}y_1\\y_0\end{bmatrix}`

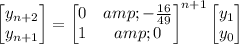
or

`\begin{bmatrix}y_n\\y_(n-1)\end{bmatrix}=\begin{bmatrix}0&-(16)/(49)\\1&0\end{bmatrix}^(n-1)\begin{bmatrix}y_1\\y_0\end{bmatrix}`

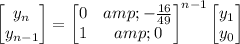
Then solving the recurrence is a matter of diagonalizing the coefficient matrix, raising to the power of
`n-1`, then multiplying by the column vector containing the initial values. The solution itself would be the entry in the first row of the resulting matrix.