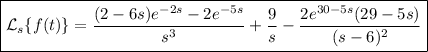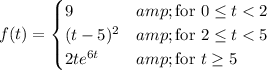
and presumably 0 for
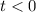 . We can express
. We can express
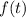 in terms of the unit step function,
in terms of the unit step function,
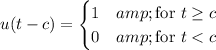
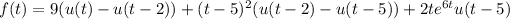
Quick explanation:
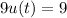 for
for
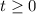 , and
, and
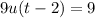 for
for
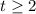 . So subtracting these will cancel the value of 9 for all
. So subtracting these will cancel the value of 9 for all
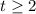 and leave us with the value of 9 over the interval we want,
and leave us with the value of 9 over the interval we want,
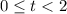 . The same reasoning applies for the other 3 terms.
. The same reasoning applies for the other 3 terms.
Recall the time displacement theorem:
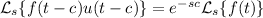
By this property, we have
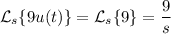

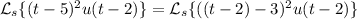
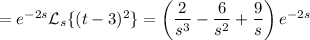
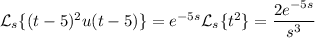
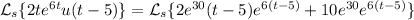
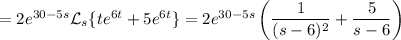
Putting everything together, we end up with