Question

Based on a​ poll, among adults who regret getting​ tattoos, 28​% say that they were too young when they got their tattoos. Assume that eight adults who regret getting tattoos are randomly​ selected, and find the indicated probability. Complete parts​ (a) through​ (d) below.

a. Find the probability that none of the selected adults say that they were too young to get tattoos.

b. Find the probability that exactly one of the selected adults says that he or she was too young to get tattoos.

c. Find the probability that the number of selected adults saying they were too young is 0 or 1.

d. If we randomly select eight ​adults, is 1 a significantly low number who say that they were too young to get​ tattoos?

Answer 1

Explanation:

Ok, so we can use the binomial distribution formula, since certain constraints are met in this case:

• each event is independent
• there is either a failure or a success
• there is a set number of trials
• the probability of success is constant (basically independence)

Binomial Distribution Formula:

`P(x)=(^n_x)*p^(x)*(1-p)^(n-x)`

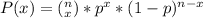
In this formula n=number of trials

p = probability of success

(1-p) = probability of failure

x = number of success

and P(x) = probability of getting "x" successes

The combination formula can be calculated using the following formula:
`(^n_k) =(n!)/(k!(n-k)!)`

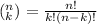
So let's define the values in the equation:

• n = 8
• p = 0.28

The x depends on the part of the question we're on, so let's start with part A:

• So in this case x=0, since the number of "successes" in this context just means how many adults regret getting a tattoo.
• So plugging in the values into the binomial distribution formula we get the following equation:
• 
  `P(0)=(8!)/(0!*(8-0)!)*0.28^0*0.72^(8-0)`
• 
  `P(0)=(8!)/(1*8!)*1*0.72^8`
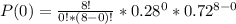
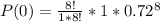
• Simplifying further we get:
• 
  `P(0)=0.72^8`
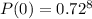
• Now just use a calculator to calculate this value:
• 
  `P(0)\approx0.0722`
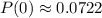
• This can also be represented as 7.22%, by multiplying this by 100

Part B:

So in this case x=1, so plugging this into the formula we get:

`P(1)=(8!)/(1!*(8-1)!)*0.28^1*0.72^(8-1)\\\\P(1)=(8*7!)/(7!)*0.28*0.72^7\\P(1)\approx 8*0.28*0.1003\\P(1)\approx 0.2247`

This can also be represented as 22.47%

Part C:

So in this case, all we really have to do is add the probabilities, as you may recall the formula:
`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

In this case, it's mutually exclusive, because there is no chance of getting 0 and 1 at the same time, so the probability of P(A and B) is just 0, so we simplify the equation to:
`P(A\cup B)=P(A)+P(B)`

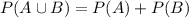
So adding the two probabilities calculated in the previous questions we get:
`P(x\le1)\approx 0.2247+0.0722\\P(x\le1) \approx 0.2969`

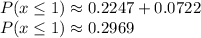
The probability can also be represented as 29.69%

Part D:

As calculated in one of the previous parts, the probability is approximately 22%, which isn't significantly low and has around a 1/5 chance of occurring so if this were to occur, there is no reason to suspect that the probabilities are incorrect.