Explanation:
Ok, so we can use the binomial distribution formula, since certain constraints are met in this case:
- each event is independent
- there is either a failure or a success
- there is a set number of trials
- the probability of success is constant (basically independence)
Binomial Distribution Formula:
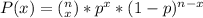
In this formula n=number of trials
p = probability of success
(1-p) = probability of failure
x = number of success
and P(x) = probability of getting "x" successes
The combination formula can be calculated using the following formula:
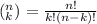
So let's define the values in the equation:
The x depends on the part of the question we're on, so let's start with part A:
- So in this case x=0, since the number of "successes" in this context just means how many adults regret getting a tattoo.
- So plugging in the values into the binomial distribution formula we get the following equation:
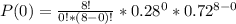
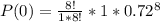
- Simplifying further we get:
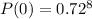
- Now just use a calculator to calculate this value:
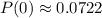
- This can also be represented as 7.22%, by multiplying this by 100
Part B:
So in this case x=1, so plugging this into the formula we get:

This can also be represented as 22.47%
Part C:
So in this case, all we really have to do is add the probabilities, as you may recall the formula:
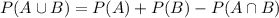
In this case, it's mutually exclusive, because there is no chance of getting 0 and 1 at the same time, so the probability of P(A and B) is just 0, so we simplify the equation to:
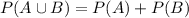
So adding the two probabilities calculated in the previous questions we get:
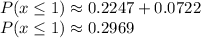
The probability can also be represented as 29.69%
Part D:
As calculated in one of the previous parts, the probability is approximately 22%, which isn't significantly low and has around a 1/5 chance of occurring so if this were to occur, there is no reason to suspect that the probabilities are incorrect.